This paper has been presented at AISTATS 2023, one of the top theory-oriented AI conferences.

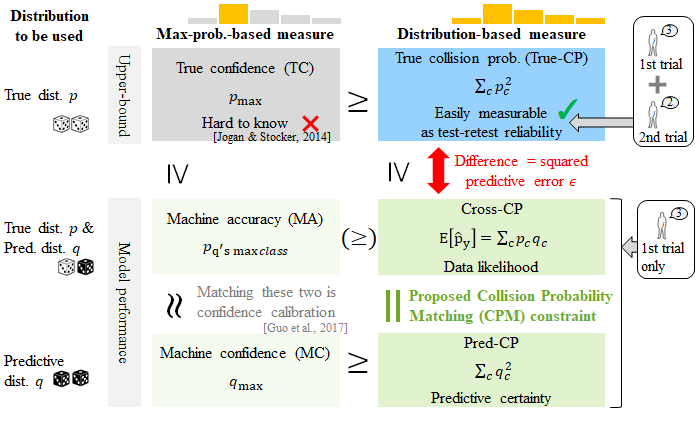
Abstract Two important aspects of machine learning, uncertainty and calibration, have previously been studied separately. The first aspect involves knowing whether inaccuracy is due to the epistemic uncertainty of the model, which is theoretically reducible, or to the aleatoric uncertainty in the data per se, which thus becomes the upper bound of model performance. As for the second aspect, numerous calibration methods have been proposed to correct predictive probabilities to better reflect the true probabilities of being correct. In this paper, we aim to obtain the squared error of predictive distribution from the true distribution as epistemic uncertainty. Our formulation, based on second-order Rényi entropy, integrates the two problems into a unified framework and obtains the epistemic (un)certainty as the difference between the aleatoric and predictive (un)certainties. As an auxiliary loss to ordinary losses, such as cross-entropy loss, the proposed collision probability matching (CPM) loss matches the cross-collision probability between the true and predictive distributions to the collision probability of the predictive distribution, where these probabilities correspond to accuracy and confidence, respectively. Unlike previous Shannon-entropy-based uncertainty methods, the proposed method makes the aleatoric uncertainty directly measurable as test-retest reliability, which is a summary statistic of the true distribution frequently used in scientific research on humans. We provide mathematical proof and strong experimental evidence for our formulation using both a real dataset consisting of real human ratings toward emotional faces and simulation.

[pdf in PMLR] [sourse code].